A robot has position and orientation. In particular, one of advantages in 6-axis robotic arm is to pose diverse orientation. This article is written for better understanding of robot orientation.

Rotation Matrix

A rotation is represented in a matrix. In Cartesian space, a robot orientation is decided by a combination of rotations in X, Y, and Z direction, and we can have a 3-by-3 rotation matrix for each orientation.

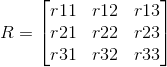
(Refer to Rotation matrix, wikipedia)

Rotation Vector

In Universal Robots, the axis-angle representation is used for robot orientation. As a brief explanation, let me assume that there is a direction vector. Around the vector, an orientation can be rotated by a certain angle, theta. As a result of rotation, we can have a different orientation. The axis-angle representation is useful for robotics calculation such as kinematics and dynamics. 

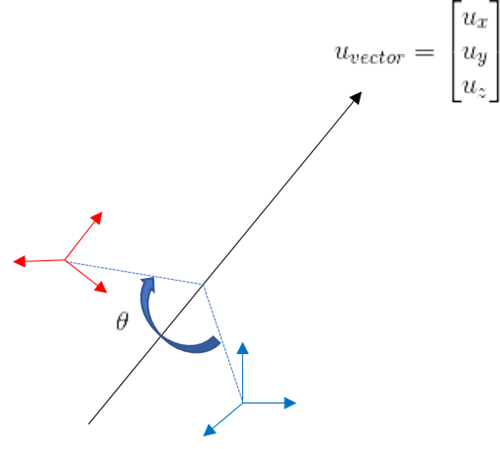
Rotation vector is a representation of the unit direction vector multiplied by the angle in the axis-angle representation.

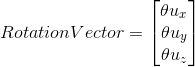
In order to define an orientation with the axis-angle representation, we need 4 values in total; three elements of unit direction vector and rotation angle. That is the reason why the values of rotation vector are not intuitive.

(Refer to Axis-angle representation, wikipedia)

RPY

You may be more familiar with roll, pitch, and yaw to represent the robot orientation. In RPY, the order of rotation should be critical. For instance, despite the same amount of angles, the result of rotation roll->pitch would be different from that of pitch->roll.

Although the rotation vector is used in Universal Robots by default, you should be able to see the RPY values in Move tab of Polyscope. In addition, you can use the URScript functions to convert the representation between RPY and rotation vector. 

rotvec2rpy(rotation vector)

rpy2rotvec(rpy vector)

Transformation Matrix

For calculation of kinematics, a transformation matrix can be defined as a 4-by-4 matrix, consisting of rotation matrix and position vector. The rotation vector and/or RPY will be converted to the rotation matrix. We can calculate the robot position and orientation based on the transformation matrix multiplication.

pose_trans() is using the principle of the transformation matrix. The calculated position and orientation is referred to the tool frame. With respect to pose_add(), the calculated position is ths sum of two position inputs, but the resulted orientation is the matrix multiplication of two rotation matrix. In other words, in pose_add(), the position is corresponding to the base frame but the orientation is referred to the tool frame.